SWF Detection | Shibaji Chakraborty

Short-wave fadeout (SWF), a transient ionospheric response to solar flares, disrupts HF communication by enhancing ionization in the D-layer, causing severe absorption of HF radio signals. This study introduces two probabilistic anomaly detection schemes for identifying SWF events generated by M and X class flares in Super Dual Auroral Radar Network (SuperDARN) observations. Leveraging statistical Z-score and nonlinear energy operators, the schemes exhibit varying performance influenced by flare intensity and scheme parameters. Remarkably, a correlation coefficient of ~0.73 is observed between monthly flare and SWF counts, underscoring the effectiveness of the Z-score scheme in detecting SWF events.

GOES and Blackstone (BKS) radar measurements during a solar flare and associated SWF event on 11 March 2015: (a) GOES X-ray flux in the 0.1–0.8 nm (red) and 0.05–0.4 nm (blue) wavelength bands and (b) number of BKS backscatter echoes. The vertical lines passing through both panels identify the peak times of X2.2 (red) and M1.0 (orange) class events.

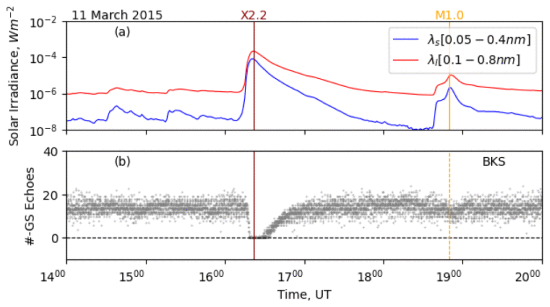
Figure illustrates Blackstone (BKS) radar measurements and GOES X-ray fluxes on March 11, 2015. The X2.2 class flare at 16:22 UT led to a rapid decrease in backscatter echoes within 10 minutes, causing a complete radio blackout followed by a gradual recovery over 30–60 minutes. The M1.0 class event initiated compoundly, with a small C-class onset around 8:40 UT followed by a larger M-class onset at 8:45 UT. While the M-class event showed a weaker response with a subtle decrease in BKS backscatter echoes, the X-class flare exhibited a distinct inverted spike, a characteristic signature of short-wave fadeout commencement. This observation aligns with previous studies, emphasizing the unique signatures associated with different flare classes.

Detection Schemes

In this study we have used two different spike detection techniques to identify SWF signatures in SuperDARN backscatter observations. First, a modified Z-score based spike detection technique, also referred as the Whitaker-Hayes algorithm, and second, a nonlinear energy operator (NEO).

A. Modified Z-score

Z-score represents how many standard deviations away a given observation is from the mean. By contrast, the modified Z-score is estimated using the median ($M$) and median absolute deviation ($MAD$) instead of mean and standard deviation. Equation \eqref{eq:zscore} presents the modified Z-score assuming the backscatter count ( $e_n$ ) is normally distributed. The multiplier 0.6745 in the equation is the 0.75 th quartile of the standard normal distribution, to which the $MAD$ converges:

\begin{equation} \label{eq:zscore} z(e_n) = 0.6745 \times \frac{e_n - e_n^M}{e_n^{MAD}} \end{equation}

where: $e^M_n$, $e^{MAD}_n$, and $z(e_n)$ are the median, median absolute deviations, and Z-score of backscatter count ($e_n$). For a spike the $z(e_n)$ value is high.

B. Nonlinear Energy Operator (NEO)

The NEO provides a measure of change in the instantaneous energy (i.e., squared magnitude of the considered signal) in the signal, here SuperDARN radar backscatter count ( $e_n$ ). Previous studies have found that NEO can discriminate between spikes and noise better than a simple thresholding detector, specifically when the signal-to-noise ratio (SNR) is low. Another study found the NEO provided more accurate spike detection than detectors and had lower computational requirements. The main goal of the NEO, defined in Equation \eqref{eq:neo} , is to emphasize the difference between spikes and noise. The NEO adapts to changes in SNR level to identify the spike in the data:

\begin{equation} \label{eq:neo} neo(e_n) = \dot{e}_n^2 - \ddot{e}_n e_n \end{equation}

where: $\dot{e}_n$, $\ddot{e}_n$, and $neo(e_n)$ are the first, second order time derivative, and spike score of backscatter count $(e_n)$ estimated using the NEO. For a spike the value of $neo(e_n)$ is high.

C. Probabilistic Detection Schemes

The algorithm applies a time window to the radar data obtained on each beam and calculates a spike score using both of the operators described in the two previous subsections. The difference between the spike score and a spike threshold is projected onto a sigmoid curve to estimate probability. The algorithm then estimates median spike probability $\mu^{(x)}$ across the beams, multiple beam detection probability $\theta^{(x)}$ , and reliability score $\gamma^{(x)}$ for all beams during that time window. The detection probability $\tau^{(x)}$ is estimated by multiplying $\mu^{(x)}$ and $\theta^{(x)}$. More details about these metrics are listed in Table I. The final output is the probability and reliability score, both of which need to be high for a successful spike detection.

Symbol	Description	Range
$\mu^{(x)}$	Median spike probability across the beam: Probability that a spike occurred.	[0-1]
$\theta^{(x)}$	Beam detection probability: Probability that a spike occurred accross multiple beams within $\Delta T$ interval.	[0-1]
$\tau^{(x)}$	Probability that a spike occurred: Probability that a spike occurred across different radar beams within $\Delta T$ interval.	[0-1]
$\gamma^{(x)}$	Reliability Score: Quantify uncertainity in $\tau^{(x)}$ estimates. A high value is expected for a reliable $\tau^{(x)}$ estimate.	[0-1]

Results/Analysis

A. Event Analysis: 11 March 2015

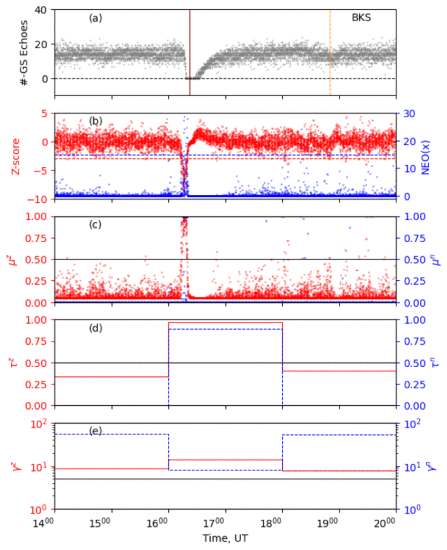
Following figure presents example results from the SWF detection scheme applied to BKS radar data obtained on 11 March, 2015. For this case, the algorithm used a time window ($\Delta T$ ) of 2 hours and spike thresholds ( $s^{th}$ ) of -3 and 15 for the Z-score and NEO operators, respectively. From top to bottom the panels show the number of backscatter echoes, spike scores, median probabilities $\mu^{(x)}$, detection probabilities $\tau^{(x)}$, and reliability scores.

Results from the SWF detection scheme applied to BKS radar data obtained on 11 March, 2015: (a) number of BKS backscatter echoes, (b) spike scores, (c) median probabilities, (d) detection probabilities within 2-hour window, and (e) reliability scores. Red and blue colors represent outputs from the Z-score and NEO operators, respectively. Red and blue horizontal lines in panel (b) represent threshold scores $$s^{th}$$ for the Z-score and NEO, respectively. Horizontal black lines passing through panels (c–d) represent threshold of detection probability 0.5, while the same for panel (e) represents threshold of detection certainty 5.

B. Statistical Analysis

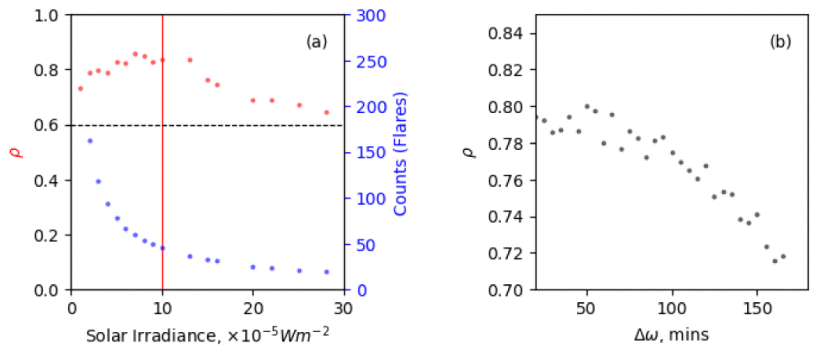
Following figure shows how the solar flare - SWF spike correlation coefficient varies with (a) minimum threshold of solar flare irradiance and (b) the length of the time window. The correlation coefficients in (a) were calculated using a fixed 2-hour time window while those in (b) used a fixed lower flare intensity threshold corresponding to M2 class. All other algorithmic parameters correspond to the same values used to generate previous figures. Panel (a) shows the correlation coefficient maximizes near a minimum flare intensity threshold corresponding to X1 class (red vertical line). Below this threshold, the correlation is lower because of the weaker SWF response to M-class flares, while above the X1 threshold the correlation becomes increasingly degraded by poor statistics. Panel (b) shows the correlation coefficient steadily decreases as the length of the time window is increased, with a much sharper rate of decrease beyond an hour or so. When the time window is too long, it is difficult to identify the SWF spikes against the background of hour-to-hour diurnal variations.

Variation of the solar flare - SWF spike correlation coefficient versus (a) solar flare irradiance, and (b) length of time window. Blue and red dots in panel (a) represent the number of flares and the correlation coefficient, respectively. The vertical red line in panel (a) corresponds to an X1-class flare. Correlation coefficients in panel (a) were calculated using a fixed time window $$\Delta T$$= 120 minutes while those in panel (b) include all flares of intensity M2 class and higher. All other algorithmic parameters are the same as described in previous figure.

Summary & Conclusion

The scheme utilizes statistical Z-score and nonlinear energy operator (NEO) based spike detection techniques to identify sudden reductions in the number of SuperDARN backscatter echoes produced by SWF. We found the Z-score method outperforms the NEO method, particularly for weaker M-class flares. The correlation was also found to decrease substantially when the time window for spike detection is longer than an hour or so. Future work includes: (1) creating a list of SWF events in the SuperDARN historical archive for wider scientific community use, and (2) developing a near real-time monitoring system for tracking the occurrence, extent, and intensity of ongoing SWF events for radio system operators.